Workshop am Kongress des VBS, August 2003 in Dortmund
Zurück zur Unterseite der AG Braille im VBS
Zurück zur Hauptseite www.braille.ch
In der Mathematikdidaktik wird seit einigen Jahren die Bedeutung der schriftlichen Rechenverfahren kontrovers diskutiert. Für die Alltagsbewältigung spielen schriftliche Rechenverfahren seit der Verbreitung des Taschenrechners kaum noch eine Rolle. Trotzdem nehmen sie nach wie vor einen großen Teil des Mathematikcurriculums der Klassen 3 und 4 der Grundschule ein.
Für blinde Menschen bekommt diese Diskussion noch einen ganz anderen Stellenwert. Schriftliche Verfahren im herkömmlichen Sinne können nur mit Hilfe einer Punktschriftmaschine ausgeführt werden (die besonderen Verfahren mit der Sticheltafel werden heute nicht mehr vermittelt und hier vernachlässigt!) In Situationen, in denen sehende Menschen auf schriftliche Rechenverfahren zurückgreifen (im Restaurant, im Supermarkt etc.) haben blinde Menschen in der Regel keine Punktschriftmaschine zur Hand. Somit spielen für sie in Alltagssituationen die Kopfrechen- und Überschlagsverfahren eine weitaus größere Rolle. Sie sind ebenso wichtig zur Überprüfung der Taschenrechnerergebnisse, um Tippfehler zu entdecken.
Trotz dieser Erkenntnisse werden schriftliche Rechenverfahren in der modernen Mathematikdidaktik propagiert und somit auch im Unterricht der Blindenschule vermittelt. Der Schwerpunkt sollte jedoch heute eher auf dem Verständnis der Algorithmen - einer Einsicht in die Verfahren - und weniger auf absoluter Rechensicherheit liegen. Hierfür sind vielfältige kreative Übungen nötig.
Im Folgenden soll die handlungsorientierte Einführung der schriftlichen Addition bis zur schriftlichen Ausführung, wie sie in einer 3. Klasse der Schloss-Schule Ilvesheim durchgeführt wurde, dargestellt werden.
Wichtige Vorkenntnisse für die Ausführung und das Verständnis der schriftlichen Addition sind eine sichere Kenntnis des 1+1, des Bündelungsprinzips und der Stellenwertschreibweise.
Als Ausgangspunkt der handlungsorientierten Erarbeitung werden Zahlen mit den Mehrsystemblöcken nach Dienes (MSB) in eine Stellenwertkiste (Karton mit 2 Reihen von je 3 Fächern) gelegt. Hierbei werden die Zahlen durch Einer-Würfel, Zehner-Stangen sowie Hunderter-Platten dargestellt.
Beispiel: 175 + 213
In den oberen Fächern: 1 Hunderter-Platte, 7 Zehner-Stangen und 5 Einer-Würfel; in den unteren Fächern: 2 Hunderter-Platten, 1 Zehner-Stange und 3 Einer-Würfel.
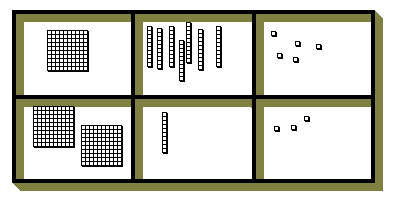
Anschließend werden diese durch Zusammenlegen addiert. Bei dieser Rechenkiste gelten 2 "geheime Regeln":
Auf diese Weise wird das spätere Übertragen in die nächste Spalte handelnd erarbeitet.
Im nächsten Schritt werden die MSB, die noch die Anzahlen konkret darstellen, durch Spielsteine ersetzt. Hier stellt derselbe Stein je nach Position einen Einer, einen Zehner resp. einen Hunderter dar.
Beispiel: 175 + 213
In den oberen Fächern: 1 Stein, 7 Steine und 5 Steine; in den unteren Fächern: 2 Steine, 1 Stein und 3 Steine.
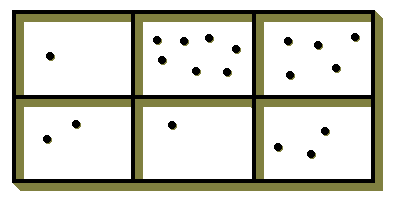
Durch verschiedene Spiele wird die Bedeutung der Position eines Steins verdeutlicht.
Analog der Arbeit mit den MSB werden anschließend durch Zusammenlegen Additionen durchgeführt. Das Umtauschen ist hierbei schwerer zu begreifen, da ja dieselben Steine benutzt werden und diese nur durch den Spaltenwechsel ihren Wert verändern (s. Vorübungen).
Mit dem nächsten Schritt erfolgt der Übergang von der enaktiven in die ikonische Ebene. Aufgaben werden mit tiefgezogenen, also unbeweglichen Punkten dargestellt; die Ergebnisse und Überträge werden mit Punkten gelegt. Die Sprechweise ist hierbei zunächst noch 6 Einer + 3 Einer ist 9 Einer ...
Der Wechsel von der ikonischen in die symbolische Ebene erfolgt mit Zahlensteckern, die in Anlehnung an die Cubarhythms oder den Wiener Rechenkasten (VzFB) angefertigt wurden. Jede Ziffer kann hierbei mittels kleiner Würfelchen in ein Raster gesteckt werden. Anfangs werden Aufgaben von den Schülern gesteckt; später können auch Aufgabenkärtchen aus Folie mit doppelseitigem Klebeband aufgeklebt und deren Lösungen darunter gesteckt werden. Das Stecksystem erleichtert die Einhaltung der Stellenspalten und die Notation von hinten, die auf der Punktschriftmaschine zu Schwierigkeiten führen.
Diese bestehen darin, den Schreibkopf genau unter die zu bearbeitende Spalte zu setzen sowie in der jeweils zweimaligen Betätigung der Rückschritttaste, um in die Spalte des nächstgrößeren Stellenwerts zu gelangen.
Daher sollten erst nach dem sicheren Verständnis des Algorithmus und der Schreibweise Aufgaben an der Punktschriftmaschine bearbeitet werden.
Es empfiehlt sich auf der Maschine Überträge nicht zu notieren, sondern diese jeweils in Gedanken als ersten Summanden der neuen Spalte in die Rechnung einzufügen. Somit wird das aufwändige Zeilenwechseln vermieden.
Der Übertrag kann - soweit eine Gedächtnisstütze notwendig ist - auf andere Art und Weise "notiert" werden. Bei der Perkins-Bogenmaschine kann beispielsweise der Griff angehoben werden, um einen noch offenen Übertrag darzustellen. Sobald der Übertrag abgearbeitet ist, wird der Griff zurückgestellt. Auch ein Gegenstand in einer Schale oder Ähnliches kann als Merkhilfe für einen Übertrag verwendet werden.
Kreative Übungsmöglichkeiten, die das Verständnis für das System fördern, sind z. B.
Nach der mehr praktisch angelegten Darstellung zum Bereich der Addition soll für die anderen Verfahren hauptsächlich auf spezifische Probleme der Bearbeitung in Punktschrift eingegangen werden.
Für die schriftliche Subtraktion wurde 1958 zur Vereinheitlichung des Verfahrens in der BRD die Durchführung des Ergänzungsverfahrens beschlossen. Hiermit sollte eine Anpassung an die Gymnasiallehrpläne erfolgen. In der heutigen, erneut entfachten Diskussion in der Mathematikdidaktik werden zwei große Probleme dieses Verfahrens genannt. (Vgl. Radatz u.a.)
Vorteile des Entbündelungsverfahrens sind dagegen:
Probleme treten dann auf, wenn die Ausgangszahl Nullen enthält, da dann 2 Entbündelungsschritte in die nächsthöhere Stelle nötig werden. Sind mehrere Subtrahenden vorhanden, müssen 2 Teilaufgaben berechnet werden.
In einigen Bundesländern ist die Wahl des Verfahrens seit einigen Jahren freigestellt.
Für die Bearbeitung in Punktschrift liegt - neben den genannten Gründen - auch aufgrund der nicht notierten Überträge eine Durchführung im Entbündelungsverfahren nahe. Die Überträge können hierbei jeweils zu Beginn einer neuen Spalte direkt abgezogen werden, sodass das Gedächtnis entlastet wird. Die hierbei einheitlich beibehaltene Rechenrichtung von oben nach unten kommt dem Lesen und der Orientierung mit den Fingern entgegen.
Bezüglich der schriftlichen Multiplikation ergeben sich kaum Veränderungen gegenüber dem Schwarzschriftverfahren. Neben dem ja bereits bei Addition und Subtraktion erprobten Rückstellen des Schreibkopfes treten keine Besonderheiten auf. Es empfiehlt sich jedoch die Nullen - beispielsweise bei der Multiplikation mit der Hunderterstelle - immer hinzuschreiben, um die Einhaltung der Stellenwertschreibweise zu erleichtern.
239 * 423
---------
00
Hinsichtlich der Bearbeitung auf der Punktschriftmaschine ist die schriftliche Division das schwierigste Verfahren, da die Notation an verschiedenen Stellen der Rechnung einen ständigen Zeilenwechsel erfordern würde. Es bietet sich daher eine Veränderung der Notationsform in Punktschrift an.
Hierbei werden die jeweiligen Ergebnisse rechts von der zu dividierenden Zahl geschrieben. Die Lösung ist also anschließend von oben nach unten zu lesen und sollte noch einmal richtig aufgeschrieben und unterstrichen werden.
Beispiel:
22645 :7 =3
21
--
16 2
14
--
24 3
21
--
35 5
35
--
0
3235
====
Neben der Berechnung von Aufgaben in schriftlichen Verfahren kann auch das Rechnen mit dem Abakus erlernt und geübt werden, da hiermit von geübten Benutzern sehr viel schneller Ergebnisse ermittelt werden können. Diese früher an Blindenschulen übliche Rechenmethode ist leider heute eher in Vergessenheit geraten und wird nur noch selten vermittelt.
Auf die hierbei verwendeten Methoden kann in diesem Rahmen nicht näher eingegangen werden. Es erscheint jedoch wichtig die verwendeten Verfahren einander anzugleichen um Verwirrung zu vermeiden. - Im herkömmlichen Abakus-Rechenverfahren werden zunächst die größeren Stellenwerte behandelt. - Es empfiehlt sich aber die Rechenrichtung der schriftlichen Verfahren beizubehalten.
Bei Berücksichtigung der dargelegten Prinzipien und Methoden und einem kreativen Umgang mit Übungsformen lassen sich schriftliche Rechenverfahren auch für blinde Kinder zu einem spannenden Unterrichtsinhalt entwickeln.
Melanie Krombach arbeitet seit 1999 als Lehrerin an der Schloss-Schule Ilvesheim hauptsächlich im Bereich Grundschule. Sie studierte an der PH Heidelberg sowohl Sonderpädagogik (Fachrichtungen Blinden- und Sprachbehindertenpädagogik und Unterrichtsfächer Mathematik und Heimat und Sachkunde) als auch Mobilitätserziehung (O&M).
Zurück zur Seitenübersicht
Zurück zur Unterseite der AG Braille im VBS
Zurück zur Hauptseite www.braille.ch
URL:
http://www.braille.ch/rechnen.htm
Letzte Änderung: 2004.04.10